Fitting growth models using predmicror

In this tutorial we will explain how to fit primary growth models to experimental data. For this lab, we will use the predmicror R package developed to accommodate all the functions we are being using in predictive microbiology workshops. The predmicror package is outside the base R functions, and the first step is load the predmicror, package with the principal predictive microbial growth models, and gslnls which is a package to fit non-linear models using non-linear least squares.

library(predmicror)

## 
##  Please cite the 'predmicror' package as: 
## Vasco Cadavez and Ursula Gonzales-Barron  (2022). predmicror: Fitting predictive microbiology models in r 
## If you have questions, suggestions, or comments 
## regarding the 'predmicror' package 
## https://github.com/fsqanalytics/predmicror

library(gslnls)
library(ggplot2)

Loading data

To conduct statistical analyses, we need to import data into R working environment. The predmicror package has incorporated datasets, and we can use the data() function to load the example datasets to the working environment. Thus, we will start by fitting a full growth model to experimental data, thus we load the growthfull.Rda dataset which is part of the predmicror package.

data(growthfull)

Now the dataset is available in the R environment, and we can print the entire dataset by typing growthfull or take a look to the first five lines by using the head().

growthfull

##    Time    logN     lnN
## 1     0 -0.1046 -0.2006
## 2     2  0.0792  0.1922
## 3     4  0.1212  0.1587
## 4     6  0.7344  1.5290
## 5     8  2.5531  5.9421
## 6    10  3.8358  8.8024
## 7    12  5.8476 13.3749
## 8    14  7.1938 16.1457
## 9    16  8.7521 20.2299
## 10   18  9.1119 20.8575
## 11   20  9.3162 21.6272
## 12   22  9.2224 20.5114
## 13   24  9.3019 21.3943

head(growthfull)

##   Time    logN     lnN
## 1    0 -0.1046 -0.2006
## 2    2  0.0792  0.1922
## 3    4  0.1212  0.1587
## 4    6  0.7344  1.5290
## 5    8  2.5531  5.9421
## 6   10  3.8358  8.8024

For data outer to predmicrorpackage, usually in .csv format, which are flat text files we use the read.csv() function to import the CSV file into R environment. Before load a dataset, its good practice to assure that the dataset is located in the working directory, thus to import a CSV file called growthfull.csv into the R environment we do it with the next code section.

growthfull <- read.csv("growthfull.csv", sep=";", header=TRUE)

We have the dataset in the R environment, thus we can start checking the data proprieties. For example, the str() function gives information considering the structure of the variables (numeric, integer, etc.), and the names() function show us the variables names.

str(growthfull)

## 'data.frame':    13 obs. of  3 variables:
##  $ Time: int  0 2 4 6 8 10 12 14 16 18 ...
##  $ logN: num  -0.1046 0.0792 0.1212 0.7344 2.5531 ...
##  $ lnN : num  -0.201 0.192 0.159 1.529 5.942 ...

names(growthfull)

## [1] "Time" "logN" "lnN"

Plotting data

To check the relationship between Time and lnN, we might use the function plot(), and we can check the data by visual inspection.

plot(lnN ~ Time, data=growthfull,
     xlab="Time (hours)", ylab="ln N",
     xlim=c(0,20), ylim=c(0,22))

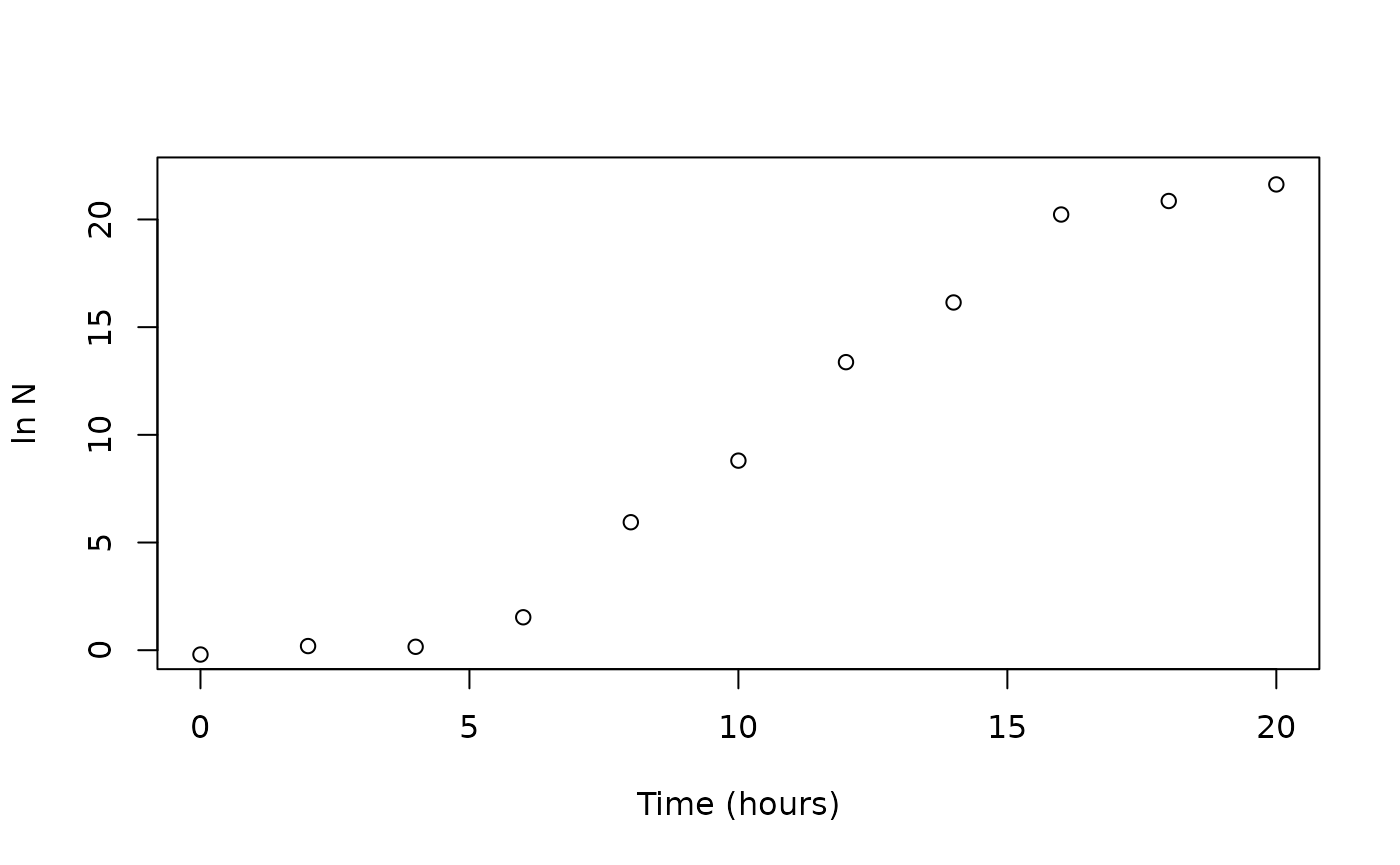
To save the plot as an .png object, we can use the png() function.

png("growthfull.png")
plot(lnN ~ Time, data=growthfull,
    xlab="Time (hours)", ylab="ln N",
    xlim=c(0,20), ylim=c(0,22))
dev.off()

Fitting the Huang full model

We will start by fitting the Huang full growth model to experimental data stored in the growthfull dataset. The Huang full growth model function (Huang()) from the predmicror package and this function will be fitted to data non-linear least squares function gsl_nls() implemented in the gslnls package. First, we need a good guess for the starting values for the fitting procedure:

start_values=list(Y0=0.02, Ymax=22, MUmax=1.6, lag=5)

Now we can fit the model to the data growthfull:

fit <- gsl_nls(lnN ~ HuangFM(Time, Y0, Ymax, MUmax, lag),
             data=growthfull,
             start=start_values)

Next, we can check the model parameters:

summary(fit)

## 
## Formula: lnN ~ HuangFM(Time, Y0, Ymax, MUmax, lag)
## 
## Parameters:
##       Estimate Std. Error t value Pr(>|t|)    
## Y0     0.04562    0.25768   0.177    0.863    
## Ymax  21.13232    0.22393  94.372 8.54e-15 ***
## MUmax  1.85942    0.06076  30.601 2.08e-10 ***
## lag    5.07987    0.25000  20.320 7.89e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4444 on 9 degrees of freedom
## 
## Number of iterations to convergence: 6 
## Achieved convergence tolerance: 3.377e-12

coef(fit)

##         Y0       Ymax      MUmax        lag 
##  0.0456246 21.1323152  1.8594243  5.0798660

The predict() function from the gslnls package can be used to produce both confidence and prediction intervals for the prediction of lnN for a given Time.

newTimes <- data.frame(Time=seq(0, 24, by=0.1))
fits <- data.frame(predict(fit, newdata = newTimes, interval="confidence", level=0.95))
str(fits)

## 'data.frame':    241 obs. of  3 variables:
##  $ fit: num  0.0456 0.0456 0.0456 0.0456 0.0456 ...
##  $ lwr: num  -0.0986 -0.0986 -0.0986 -0.0986 -0.0986 ...
##  $ upr: num  0.19 0.19 0.19 0.19 0.19 ...

preds <- data.frame(predict(fit, newdata = newTimes, interval="prediction", level=0.95))
str(preds)

## 'data.frame':    241 obs. of  3 variables:
##  $ fit: num  0.0456 0.0456 0.0456 0.0456 0.0456 ...
##  $ lwr: num  -0.97 -0.97 -0.97 -0.97 -0.97 ...
##  $ upr: num  1.06 1.06 1.06 1.06 1.06 ...

Plot the observed data with the fitted values and confidence interval

plot(newTimes$Time, fits$fit, type="l", col="blue",
     xlab="time (days)", ylab="logN",
     main="Huang full model")
points(growthfull$Time, growthfull$lnN)
lines(newTimes$Time, fits$upr, col="red")
lines(newTimes$Time, fits$lwr, col="red")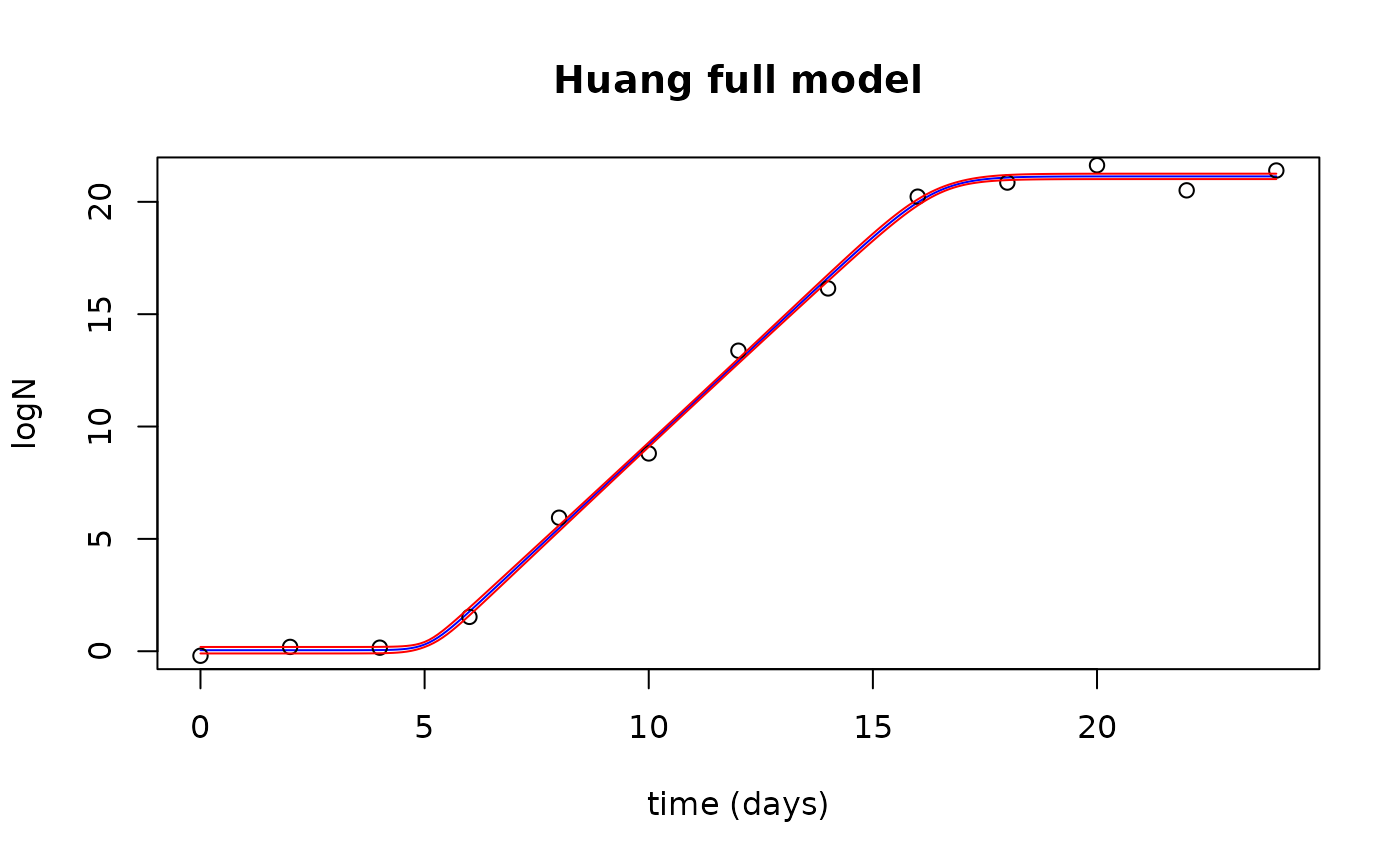

Plot the observed data with the fitted values and prediction interval

plot(newTimes$Time, fits$fit, type="l", col="blue",
     xlab="time (days)", ylab="logN", ylim=c(-1,22), xlim=c(0,24),
     main="Huang full model")
points(growthfull$Time, growthfull$lnN)
lines(newTimes$Time, preds$upr, col="red")
lines(newTimes$Time, preds$lwr, col="red")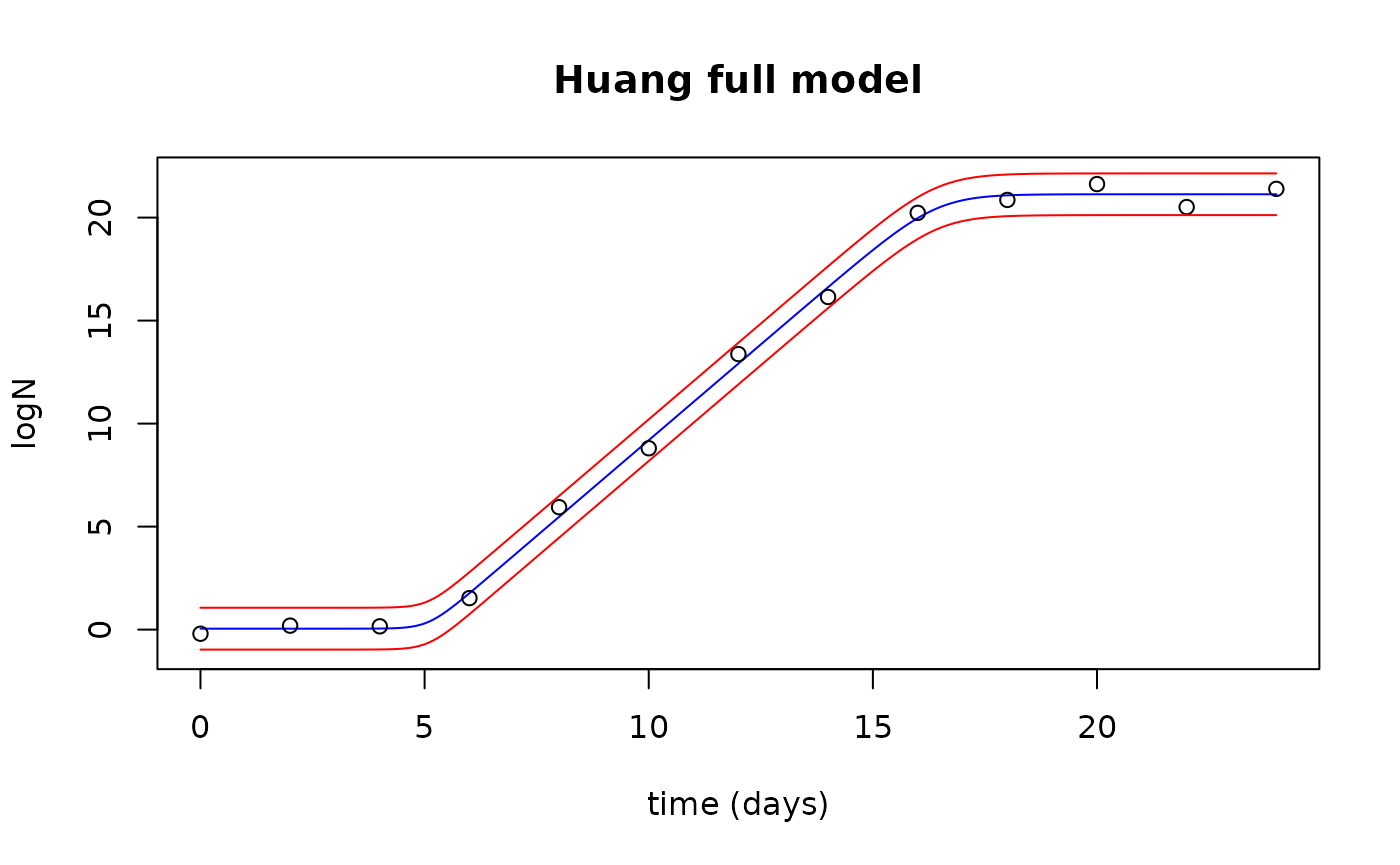

Fitting the Fang no lag model

First, we want to load the data set:

data(growthnolag)
growthnolag

##    Time   logN     lnN
## 1     0 0.7344  1.5290
## 2     2 2.5531  5.9421
## 3     4 3.8358  8.8024
## 4     6 5.8476 13.3749
## 5     8 7.1938 16.1457
## 6    10 8.7521 20.2299
## 7    12 9.1119 20.8575
## 8    14 9.3162 21.6272
## 9    16 9.2224 20.5114
## 10   18 9.3019 21.3943

Let’s start with the Fang model, fit the model to the experimental data using nonlinear least squares function gsl_nls() implemented in the gsl_nls R package:

start_values=list(Y0=0.01, Ymax=22, MUmax=1.6)
fit <- gsl_nls(lnN ~ FangNLM(Time, Y0, Ymax, MUmax),
             data=growthnolag,
             start=start_values)
fit

## Nonlinear regression model
##   model: lnN ~ FangNLM(Time, Y0, Ymax, MUmax)
##    data: growthnolag
##     Y0   Ymax  MUmax 
##  1.758 21.132  1.859 
##  residual sum-of-squares: 1.678
## 
## Algorithm: multifit/levenberg-marquardt, (scaling: more, solver: qr)
## 
## Number of iterations to convergence: 5 
## Achieved convergence tolerance: 1.414e-11

Next, we can check the model parameters:

summary(fit)

## 
## Formula: lnN ~ FangNLM(Time, Y0, Ymax, MUmax)
## 
## Parameters:
##       Estimate Std. Error t value Pr(>|t|)    
## Y0     1.75827    0.36368   4.835  0.00189 ** 
## Ymax  21.13234    0.24673  85.650 7.79e-12 ***
## MUmax  1.85922    0.06619  28.091 1.86e-08 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4896 on 7 degrees of freedom
## 
## Number of iterations to convergence: 5 
## Achieved convergence tolerance: 1.414e-11

Next, we can extract the model parameters and apply the model to new data

newTimes <- data.frame(Time=seq(0, 18, by=0.1))
fits <- data.frame(predict(fit, newdata = newTimes, interval="confidence", level=0.95))
str(fits)

## 'data.frame':    181 obs. of  3 variables:
##  $ fit: num  1.76 1.94 2.13 2.32 2.5 ...
##  $ lwr: num  1.53 1.72 1.91 2.1 2.29 ...
##  $ upr: num  1.99 2.17 2.35 2.53 2.72 ...

preds <- data.frame(predict(fit, newdata = newTimes, interval="prediction", level=0.95))

Plot the observed data with the fitted values and confidence interval

plot(newTimes$Time, fits$fit, type="l", col="blue",
     xlab="time (days)", ylab="logN",
     main="Fang no lag model")
points(growthnolag$Time, growthnolag$lnN)
lines(newTimes$Time, fits$upr, col="red")
lines(newTimes$Time, fits$lwr, col="red")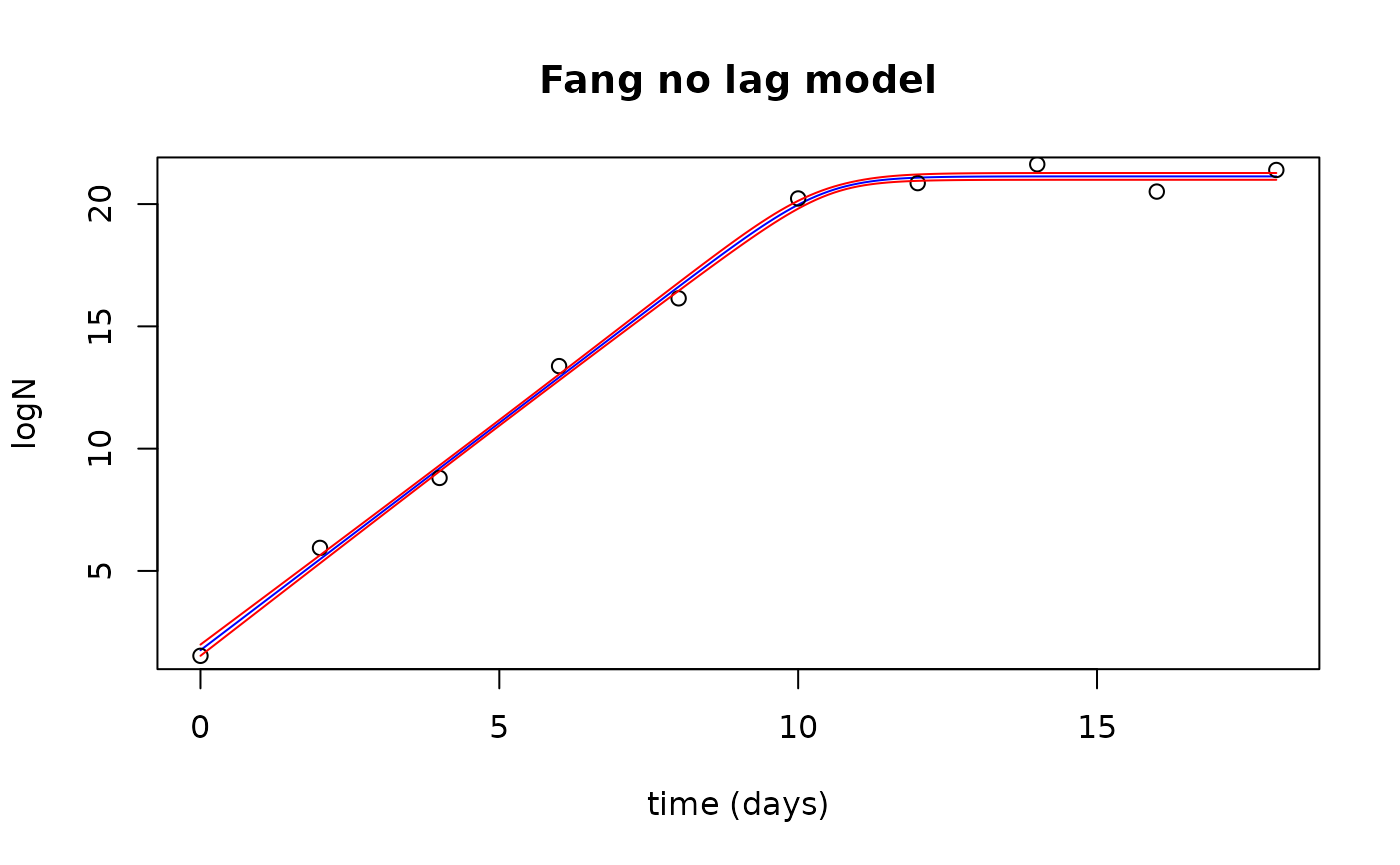

Plot the observed data with the fitted values and prediction interval

plot(newTimes$Time, fits$fit, type="l", col="blue",
     xlab="time (days)", ylab="logN", ylim=c(-1,22), xlim=c(0,18),
     main="Fang no lag model")
points(growthnolag$Time, growthnolag$lnN)
lines(newTimes$Time, preds$upr, col="red")
lines(newTimes$Time, preds$lwr, col="red")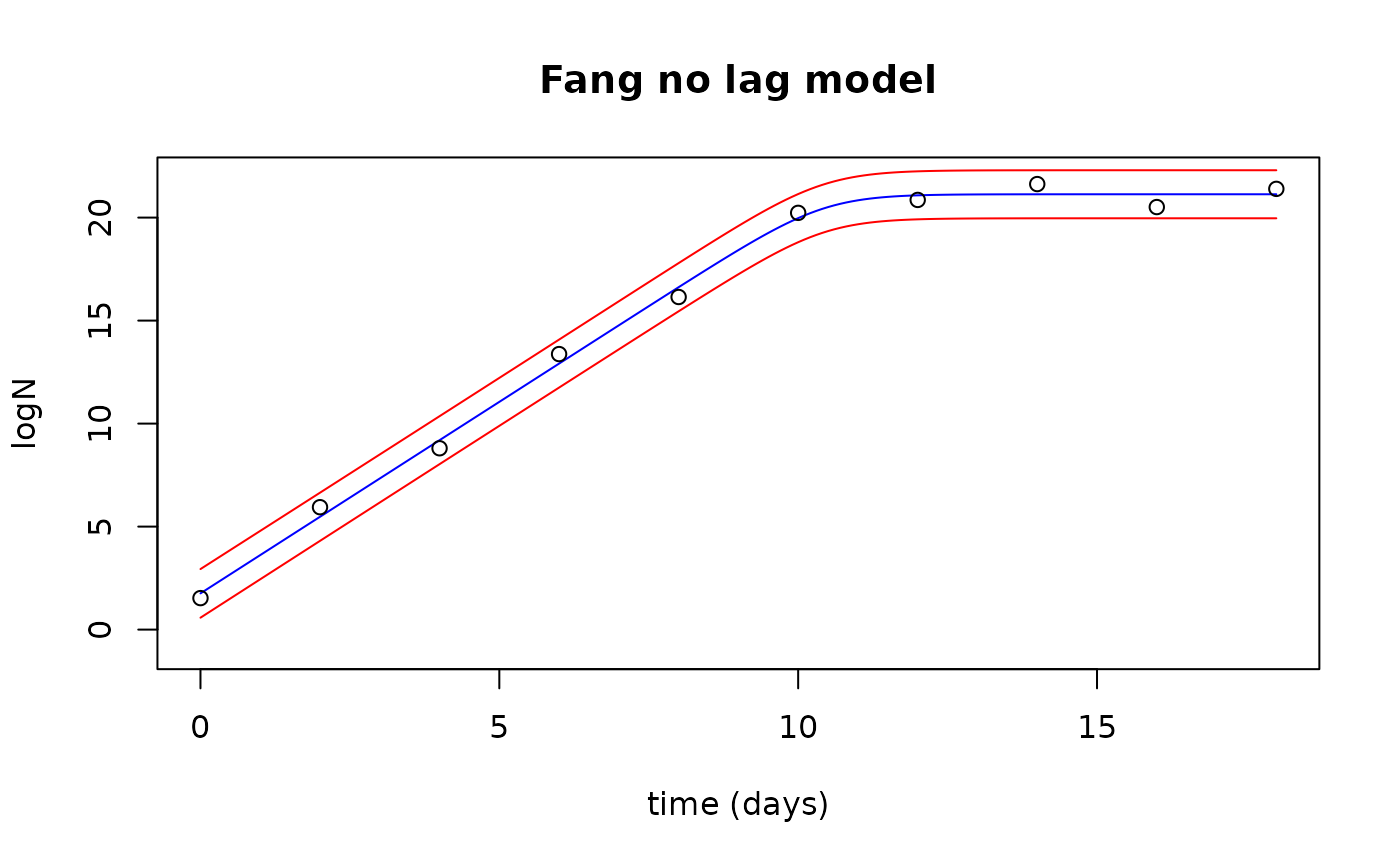

Fitting the Buchanan reduced model

First, we want to load the data set:

data(growthred)
growthred

##   Time    logN     lnN
## 1    0 -0.1046 -0.2006
## 2    2  0.0792  0.1922
## 3    4  0.1212  0.1587
## 4    6  0.7344  1.5290
## 5    8  2.5531  5.9421
## 6   10  3.8358  8.8024
## 7   12  5.8476 13.3749
## 8   14  7.1938 16.1457
## 9   16  8.7521 20.2299

Let’s start with the Buchanan model, fit the model to the experimental data using nonlinear least squares function gsl_nls() implemented in the gslnls R package:

start_values=list(Y0=0.01, MUmax=1.6, lag=5)
fit <- gsl_nls(lnN ~ BuchananRM(Time, Y0, MUmax, lag),
             data=growthred,
             start=start_values)

Next, we can check the model parameters:

summary(fit)

## 
## Formula: lnN ~ BuchananRM(Time, Y0, MUmax, lag)
## 
## Parameters:
##       Estimate Std. Error t value Pr(>|t|)    
## Y0     0.05010    0.22810    0.22    0.833    
## MUmax  1.83840    0.04722   38.93 1.92e-08 ***
## lag    5.04160    0.21567   23.38 4.02e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.3951 on 6 degrees of freedom
## 
## Number of iterations to convergence: 3 
## Achieved convergence tolerance: 5.878e-11

Next, we can extract the model parameters and apply the model to new data

newTimes <- data.frame(Time=seq(0, 16, by=0.1))
fits <- data.frame(predict(fit, newdata = newTimes, interval="confidence", level=0.95))
str(fits)

## 'data.frame':    161 obs. of  3 variables:
##  $ fit: num  0.0501 0.0501 0.0501 0.0501 0.0501 ...
##  $ lwr: num  -0.0853 -0.0853 -0.0853 -0.0853 -0.0853 ...
##  $ upr: num  0.185 0.185 0.185 0.185 0.185 ...

preds <- data.frame(predict(fit, newdata = newTimes, interval="prediction", level=0.95))

Plot the observed data with the fitted values and confidence interval

plot(newTimes$Time, fits$fit, type="l", col="blue",
     xlab="time (days)", ylab="logN",
     main="Buchanan reduced model")
points(growthred$Time, growthred$lnN)
lines(newTimes$Time, fits$upr, col="red")
lines(newTimes$Time, fits$lwr, col="red")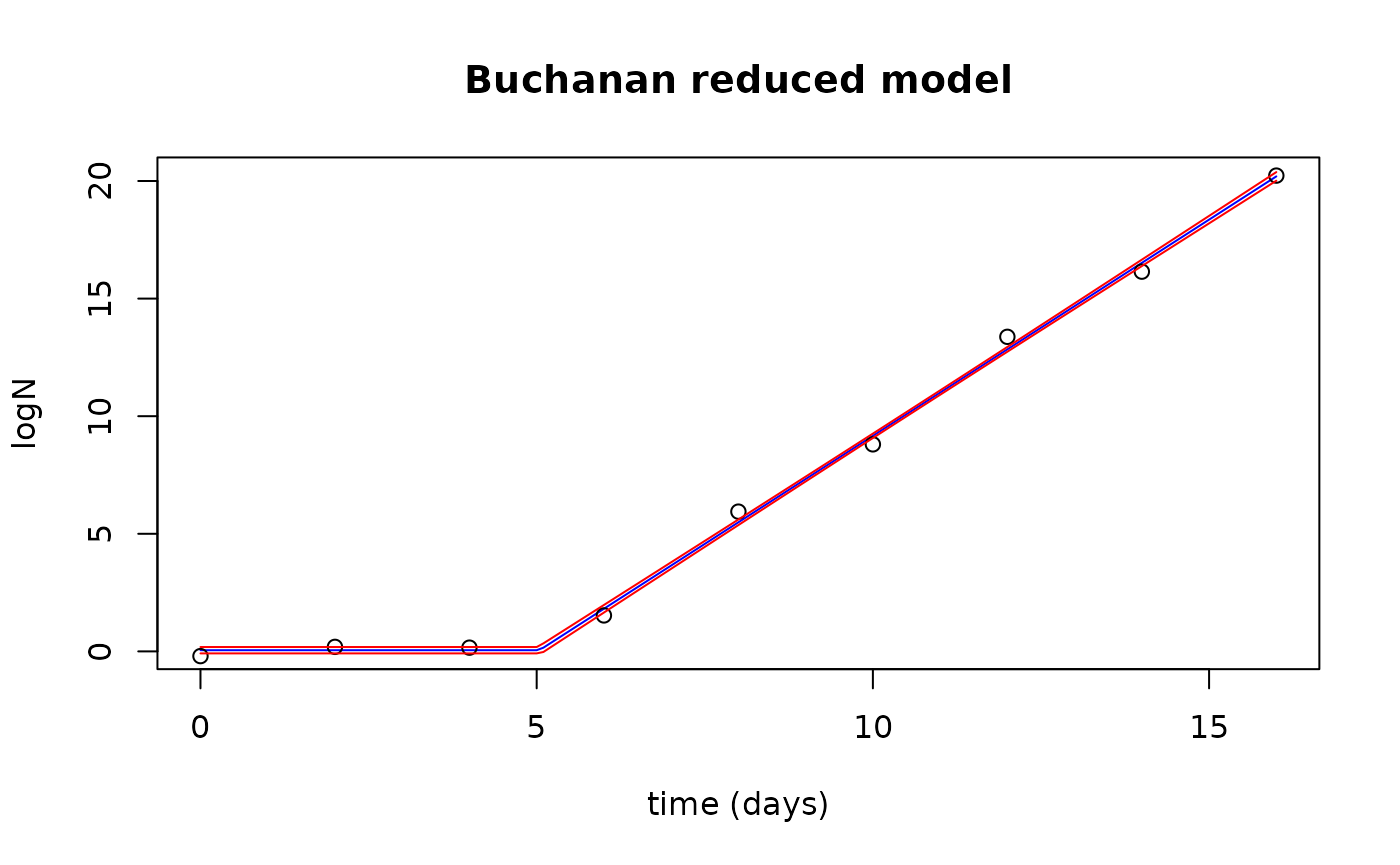

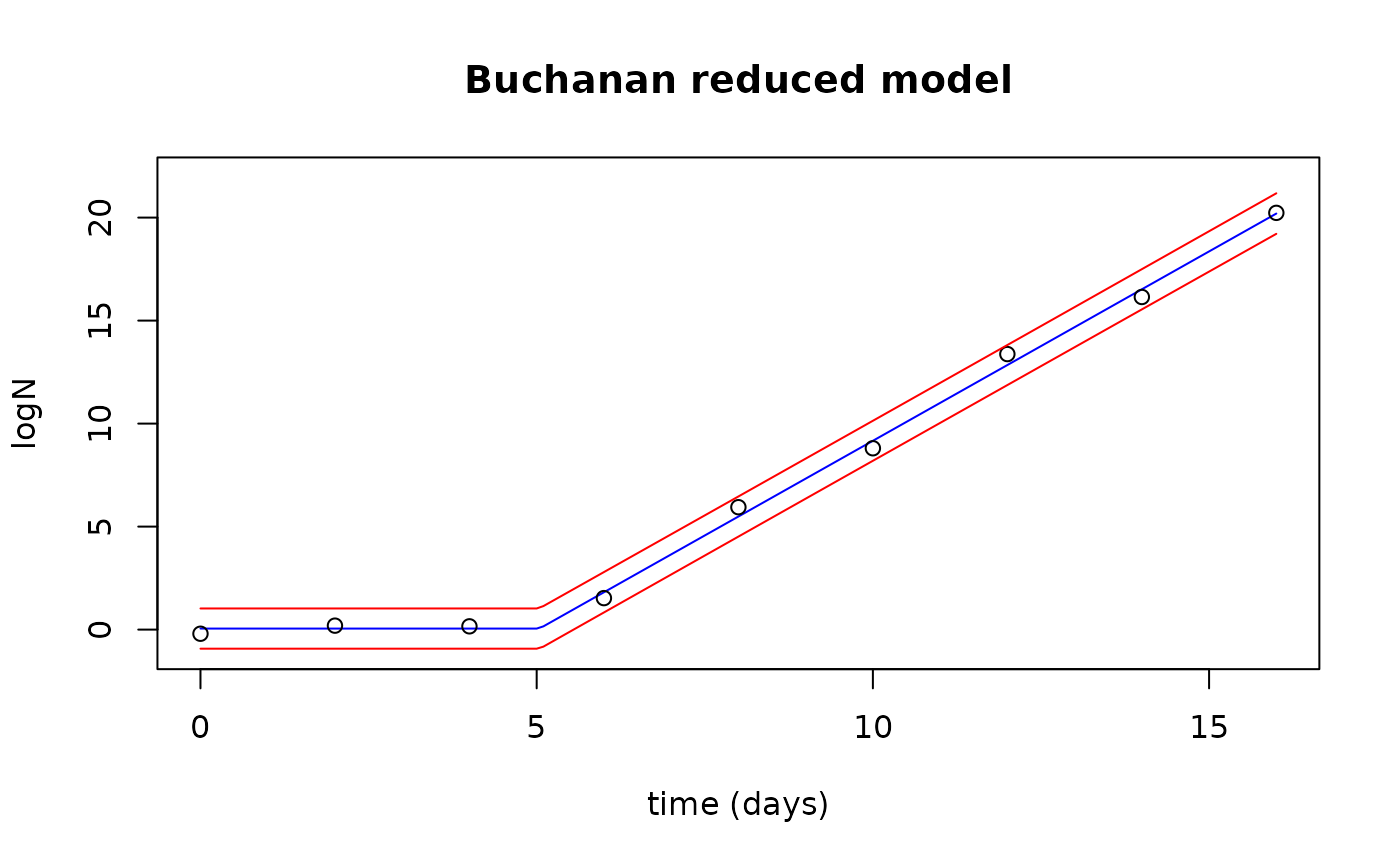
Plot the observed data with the fitted values and prediction interval

plot(newTimes$Time, fits$fit, type="l", col="blue",
     xlab="time (days)", ylab="logN", ylim=c(-1,22), xlim=c(0,16),
     main="Buchanan reduced model")
points(growthred$Time, growthred$lnN)
lines(newTimes$Time, preds$upr, col="red")
lines(newTimes$Time, preds$lwr, col="red")

Vasco Cadavez

Ursula Gonzales Barron

2022/04/30

Loading data

Plotting data

Fitting the Huang full model

Fitting the Fang no lag model

Fitting the Buchanan reduced model